Cornering: Terminology
This page is a supplement to the tip of the week on cornering skills. When discussing cornering skills, it's useful to have precise terms for the various parts and attributes of a corner. The following terms are in common use:
Attributes of a Curve
Radius
If you imagine that a curve is formed by cutting a segment out of a circle, the radius of the curve is the radius of the circle. It is a measure of how "sharp" the corner is. A large-radius curve is a long, gentle curve (often called a "sweeper") while a small-radius curve is very tight.
Constant-Radius
 Curves that are, indeed, segments of a circle are called "constant-radius" curves. City planners try to achieve constant-radius curves on city streets because they are easy to drive. On country roads, however, the road path is often determined by geography, obstacles, farmland, etc., and constant-radius curves are rare. They are also rare on racetracks, because racetrack designers deliberately try to design more challenging roads for the racers to negotiate.
Curves that are, indeed, segments of a circle are called "constant-radius" curves. City planners try to achieve constant-radius curves on city streets because they are easy to drive. On country roads, however, the road path is often determined by geography, obstacles, farmland, etc., and constant-radius curves are rare. They are also rare on racetracks, because racetrack designers deliberately try to design more challenging roads for the racers to negotiate.
Changing-Radius
Most curves you will encounter, then, are changing-radius curves. The curvature changes as you pass through the curve, sometimes more than once. The simplest changing-radius curves are those where the curvature changes only once, becoming either more sharp or less sharp as the curve progresses.
 Increasing-Radius: In an increasing-radius curve, the curvature opens out as you proceed through the curve. It's as though you are driving out from the center of a spiral toward the outside. Increasing radius curves are easy to ride, and you can accelerate as you progress through the curve. For this reason, entrance ramps onto freeways are often increasing-radius curves, allowing you to accelerate to freeway speeds as you negotiate the ramp. Increasing-Radius: In an increasing-radius curve, the curvature opens out as you proceed through the curve. It's as though you are driving out from the center of a spiral toward the outside. Increasing radius curves are easy to ride, and you can accelerate as you progress through the curve. For this reason, entrance ramps onto freeways are often increasing-radius curves, allowing you to accelerate to freeway speeds as you negotiate the ramp.  Decreasing-Radius: In a decreasing-radius curve, the curvature gets tighter as you proceed through the curve, as though you were driving in toward the center of a spiral. Decreasing-radius curves are challenging to ride [and to draw!]. You must continuously increase the amount of your steering input (increase the pressure on the inside bar when countersteering) throughout the curve. Many riders get into trouble in decreasing-radius curves by entering too fast and then being surprised by the increased turn and lean requirements. Because decreasing-radius curves force traffic to slow, they are often used on freeway exit ramps. Decreasing-Radius: In a decreasing-radius curve, the curvature gets tighter as you proceed through the curve, as though you were driving in toward the center of a spiral. Decreasing-radius curves are challenging to ride [and to draw!]. You must continuously increase the amount of your steering input (increase the pressure on the inside bar when countersteering) throughout the curve. Many riders get into trouble in decreasing-radius curves by entering too fast and then being surprised by the increased turn and lean requirements. Because decreasing-radius curves force traffic to slow, they are often used on freeway exit ramps. |
Parts of Curve
Entry & Exit
The Entry of a curve is the point where the curvature of the road begins to change. (Where it changes from straight to curved in most cases.) It may be the point where you begin steering your bike to follow the curve, although you might start your steering input slightly before or after the entry.
The Exit is the point where the road has straightened out and, under most circumstances, where you will have your bike upright and travelling in a straight line, finished with turning.
Outside & Inside
Imagine, for a moment, that a curve is formed by cutting a segment out of a circle. The inside of the curve is that part of the lane closest to the center of the circle. This is the right side of the lane for a right-hand curve, and the left side of the lane for a left-hand curve.
The outside of the curve is that part of the lane farthest from the center of the circle. This is the left side of the lane for a right-hand curve, and the right side of the lane for a left-hand curve.
Apex
The apex of the curve is the point at which half of the curvature is "used up". This may seem like a strange definition - isn't the apex just of the middle of the curve? The apex is, indeed, the middle for a constant-radius curve. However, the apex will be beyond the middle for a decreasing-radius curve, and before the middle for an increasing-radius curve. A useful definition for riding is that the apex is the point at which, looking ahead, you can first see a clear path to the exit.

Camber
Camber is a measure of the "Slope" of the road surface. Zero-Camber or Neutral-Camber means the road is perfectly flat. Positive Camber means the road is tilted, with the lower side close to the center of the curve. Positive Camber curves are easy to ride because the positive camber helps fight the sideways forces on the tires, and reduces the amount the bike has to lean. Traditional oval-shaped automobile racetrack curves, like Indianapolis, usually have Positive Camber ("banked") curves. Negative Camber means the road is tilted away from the center of the curve. Negative Camber curves are difficult to ride because the slope increases the sideways pressure on the tires and increases the lean angle of the bike. Many riders feel quite uncomfortable on Negative Camber curves.
RACING LINE
The Racing Line
The following diagram, Fig. 1, describes the racing line through a typical corner. The car is traveling from the bottom of the page through the corner. Note that the car is making a much larger radius than the actual radius of the corner
Why is the racing line above the fastest?
Decreasing Radius Turn
Increasing Radius Turn
Series of Turns
When driving through a series of turns, remember that you are looking for exit speed out of the turn, or in this case, turns. Set the car up to take the fastest exit out of the last turn. This will generally, but not always mean taking very late apexes in the first turns of the series. There are too many variations to describe here so no diagram is useful.
Inclines and Declines
This is simple. Remember that the actual braking force or cornering force that a car will generate varies directly to any hill that it is negotiating. Going uphill, the car stops much quicker and will generate more cornering force. Downhill is, of course, the opposite.
positive & negative camber
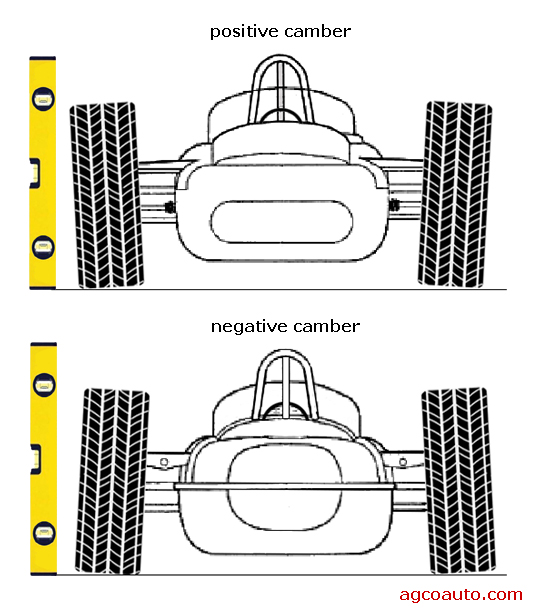
The negative camber will give our wheel more grip through the corner.
'SAAB' 카테고리의 다른 글
| [스크랩] History of saab (0) | 2011.01.25 |
|---|---|
| [스크랩] Re:언더스티어와 오버스티어 ^^ (0) | 2010.12.03 |
| [스크랩] [참고]브레이크서보, 마스터실린더 (0) | 2010.11.26 |
| [스크랩] Turbo의 선택 [Compressor map. Saab 9-5 2.3 CFM] (1) | 2010.09.20 |
| [스크랩] 터보차저의 성능 (0) | 2010.09.15 |